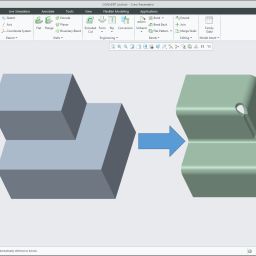
Jedną z zalet projektowania w parametrycznym systemie 3D CAD, jakim jest Creo Parametric, jest możliwość definiowania różnorodnych zależności pomiędzy wartościami wymiarów lub między wymiarami i parametrami. Możemy dzięki temu zaprojektować model, który będzie się zachowywał w sposób przewidywalny po wprowadzeniu różnych zmian. Do wprowadzenia powiązań pomiędzy różnymi wielkościami opisującymi model parametryczny możemy zastosować równania i funkcje matematyczne, noszące w Creo Parametric nazwę Relacji (Relations). Podstawowe możliwości zastosowania równań matematycznych do sterowania geometrią możemy przedstawić na przykładzie sprężyny.

Zapoznaj się z treścią tego artykułu w postaci nagrania:
Projektowanie sprężyny w Creo Parametric
Do stworzenia geometrii sprężyny w Creo Parametric wykorzystujemy funkcję Przeciągnięcia śrubowego (Helical Sweep). Jest to narzędzie, które w prosty sposób umożliwia nam zdefiniowanie przeciągnięcia po trajektorii śrubowej, przez co idealnie nadaje się do projektowania sprężyn oraz gwintów.
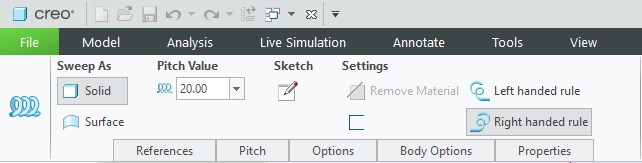
Aby zbudować geometrię sprężyny, musimy zdefiniować trzy podstawowe elementy: jej długość, skok oraz kształt i rozmiar profilu przeciąganego po linii śrubowej. W przypadku sprężyny zastosujemy zwykły profil okrągły. Możemy też określić, czy nasza sprężyna będzie prawoskrętna, czy lewoskrętna. W ten sposób, szybko i prosto, tworzymy podstawową geometrię sprężyny.
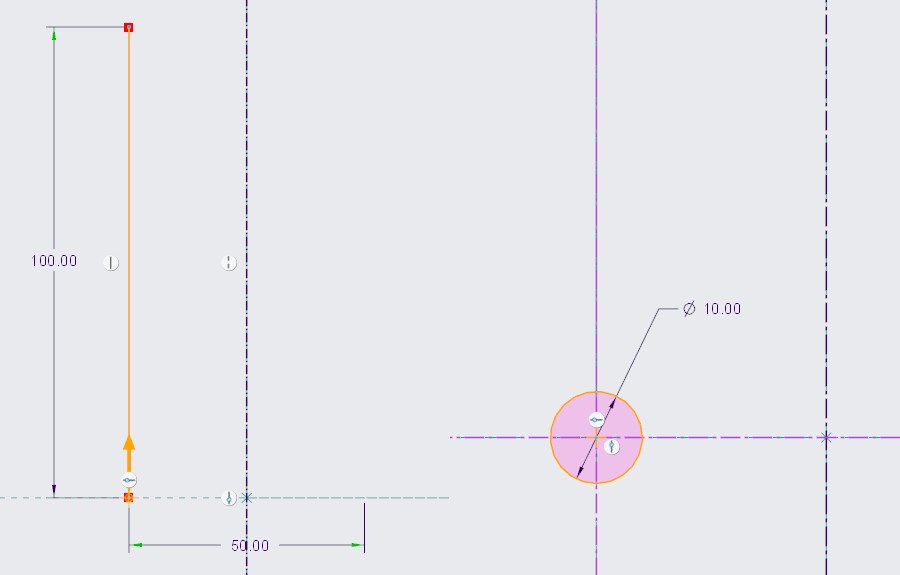
Jednak tak zaprojektowana geometria ma jedną wadę: ponieważ nie określamy w projekcie liczby zwojów, zmiana skoku lub długości sprężyny spowoduje zwiększenie liczby zwojów, ponieważ liczba ta jest wartością pochodną długości i skoku. Dlatego też wykorzystamy relacje, aby zdefiniować na stałe liczbę zwojów i uzyskać efekt rozciągnięcia lub ściśnięcia sprężyny w zależności od wprowadzonej długości.
Definiowanie relacji matematycznych
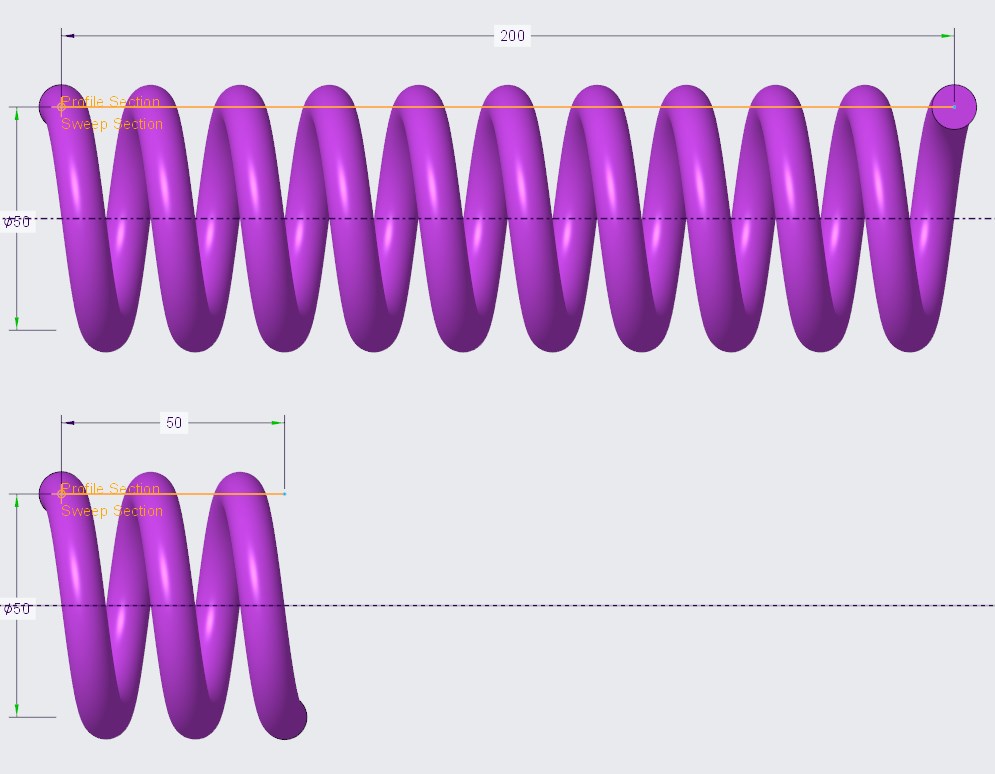
Równania matematyczne definiujemy w oknie Relacje (Relations), które możemy włączyć z poziomu grupy Założenia modelu (Model Intent). Gdy pojawi się edytor, zaznaczamy geometrię, którą chcemy sterować, aby zobaczyć wszystkie wymiary nią sterujące. Warto tutaj zwrócić uwagę, że wymiary są zaprezentowane w formie oznaczeń symbolicznych, a nie wartości liczbowych. Każdy wymiar geometrii w modelu Creo Parametric ma przypisany własny identyfikator, dzięki czemu można łatwo odnieść się do jego wartości.
Ponieważ nasza sprężyna ma długość 100 mm i skok 20, łatwo obliczyć, że liczba zwojów wynosi 5 i właśnie tę wartość przyjmiemy jako podstawę do zdefiniowania dalszej relacji. Zatem zapisujemy naszą podstawową relację:
D2 = D1/5
w której:
D1 – długość sprężyny,
D2 – wymiar skoku sprężyny,
5 – liczba zwojów.
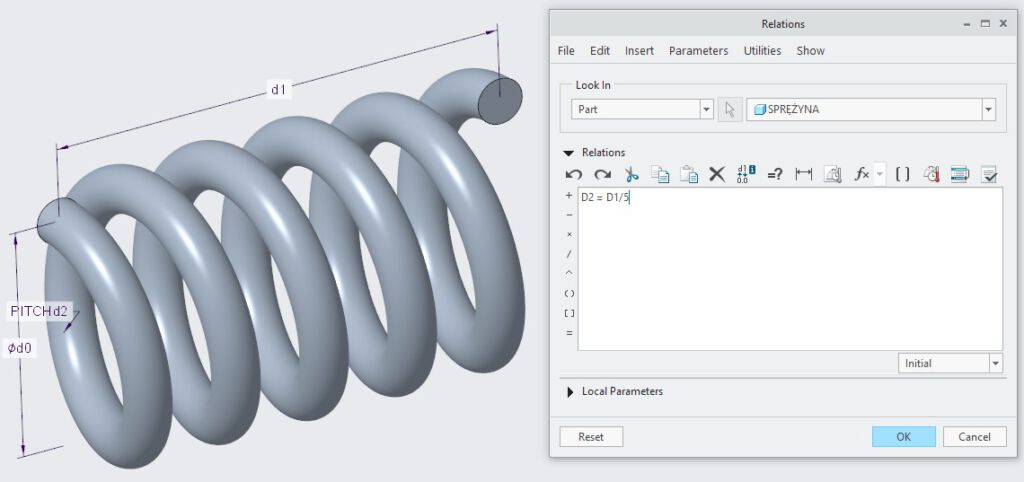
W ten sposób, niezależnie od zdefiniowanej długości sprężyny, liczba zwojów pozostanie stała, przez co uzyskamy odpowiedni efekt rozciągnięcia i ściśnięcia sprężyny.
Zwiększenie czytelności relacji
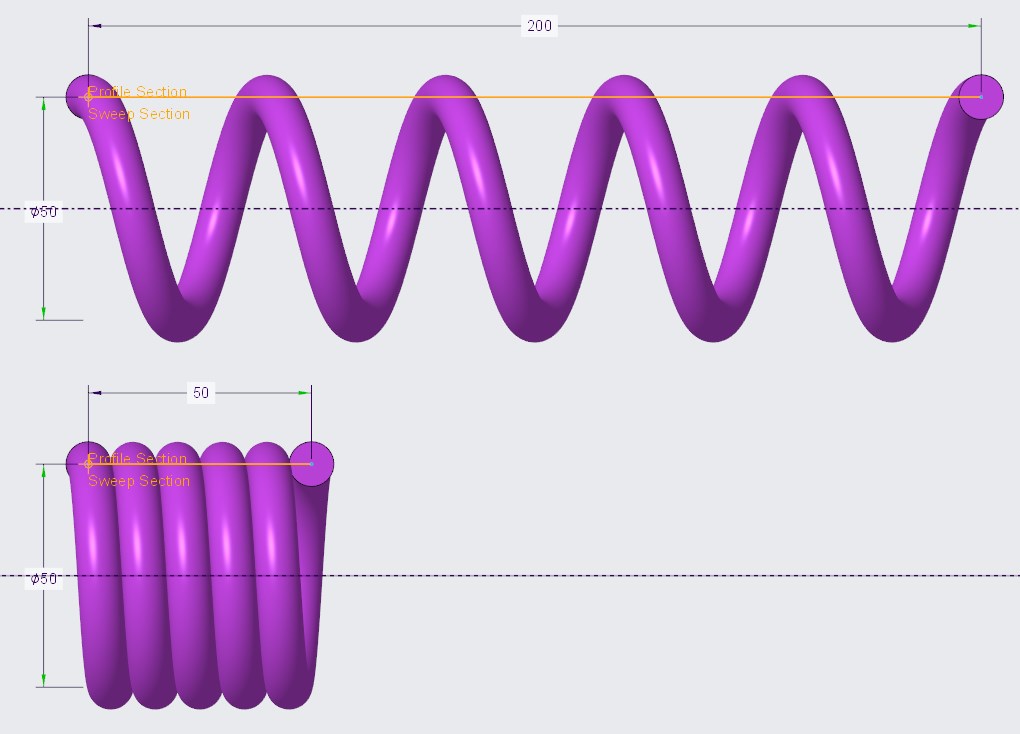
Tak zapisane relacje są jednak mało czytelne, zwłaszcza dla innego użytkownika, który pracowałby z takim modelem. Dlatego też możemy podnieść czytelność zapisu, definiując własne nazwy dla poszczególnych wymiarów, które wykorzystujemy w zapisanych już relacjach. Użyjemy więc funkcji Edytuj wymiary (Edit Dimensions), żeby wyświetlić wymiary sterujące geometrią sprężyny. Po zaznaczeniu wymiaru długości we wstążce Creo Parametric pojawi się dodatkowa zakładka Wymiar (Dimension), w której dostępne są wszystkie właściwości zaznaczonego wymiaru. Zmieńmy w tej zakładce oznaczenie wymiaru z d1 na dlugosc_sprezyny. W podobny sposób zmieniamy też oznaczenie wymiaru skoku z d2 na skok_sprezyny. Co więcej, zmiany te są automatycznie odzwierciedlane w edytorze relacji, dzięki czemu unikamy ręcznego nanoszenia poprawek, a zapis relacji staje się znacznie bardziej czytelny i zrozumiały.
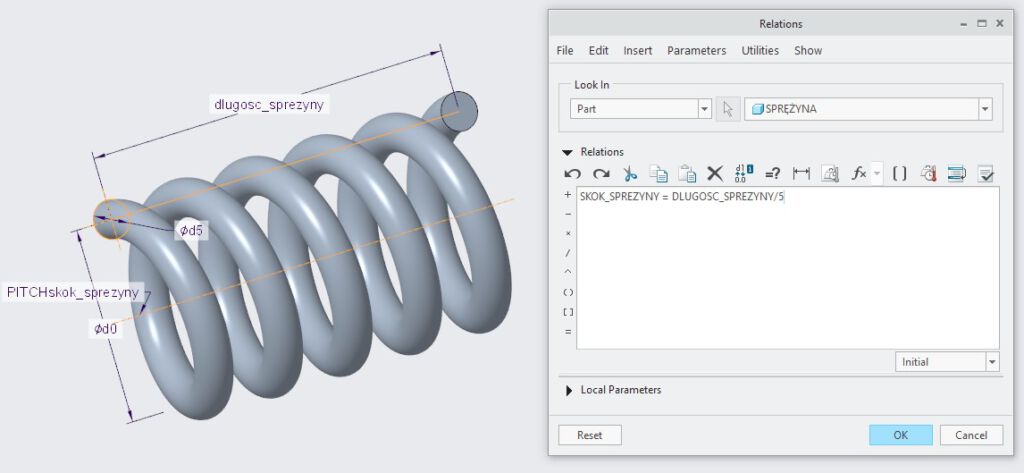
Dodanie parametru do sterowania modelem
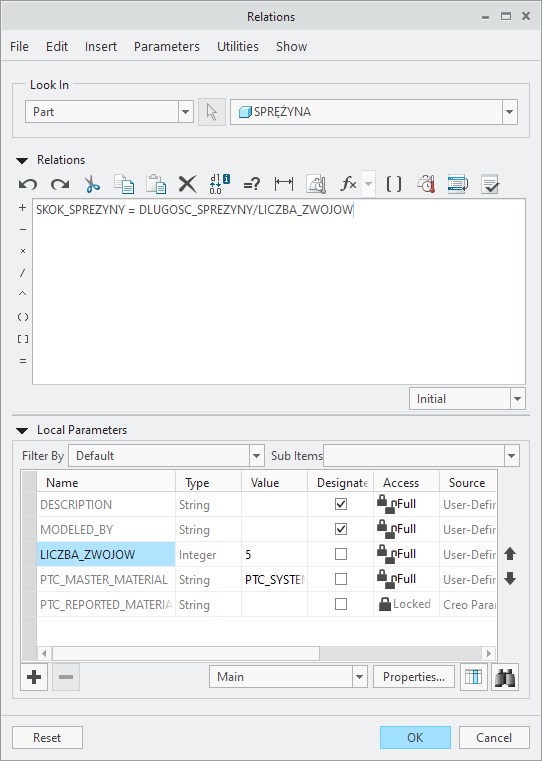
Oprócz samych wymiarów, w relacjach możemy też zastosować dodatkowe wartości w postaci parametrów modelu. Dzięki takiemu rozwiązaniu możemy wprowadzić do sterowania modelem wielkości, które nie wynikają bezpośrednio z projektowanej geometrii. W przypadku omawianej przez nas sprężyny dobrym przykładem może być liczba zwojów, którą trzeba było określić ręcznie. Zamiast wpisywać ją bezpośrednio w relacji, możemy stworzyć dodatkowy parametr, którego wartość będzie określała tę liczbę. Ponieważ liczba zwojów nie może być liczbą ułamkową, jako typ parametru zastosujemy Liczbę całkowitą (Integer). Następnie wystarczy wprowadzić nazwę parametru w miejsce dotychczasowej liczby zwojów, żeby zyskać możliwość znacznie łatwiejszego sterowania liczbą zwojów. Aby zmienić liczbę zwojów sprężyny wystarczy bowiem tylko zmienić wartość parametru, dzięki czemu nie jest konieczne odszukiwanie odpowiedniej wartości w relacji.
Dodatkowe instrukcje warunkowe
Oprócz podstawowych równań matematycznych, definiując relacje możemy też stosować dodatkowe funkcje i instrukcje. W dotychczas zdefiniowanych relacjach brakuje dodatkowego warunku określającego, jak ma się zachować sprężyna, gdy wartość skoku stanie się mniejsza od średnicy przekroju. W domyślnej sytuacji doprowadzimy do przenikania się materiału sprężyny, czego raczej nie doświadczymy w rzeczywistości.
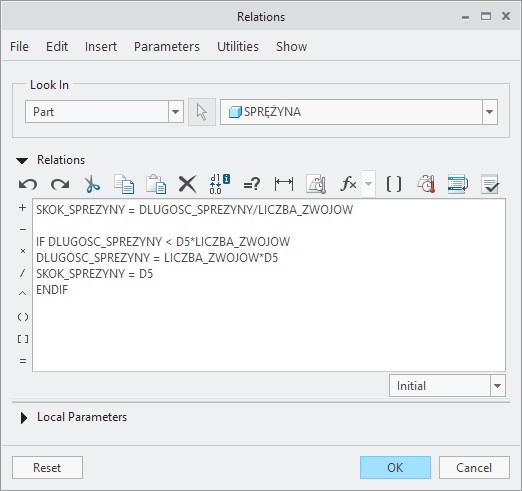
Aby zabezpieczyć się przed takim przypadkiem, zdefiniujemy dodatkowy warunek, który będzie stosowany tylko wtedy, gdy podana długość sprężyny będzie mniejsza od iloczynu skoku i średnicy. Wykorzystamy do tego instrukcję IF. Instrukcja IF (jeżeli) umożliwia nam określenie, jakie relacje należy zastosować, gdy zostaną spełnione konkretne warunki. Istotne jest, żeby zakończyć blok instrukcji poleceniem ENDIF wyznaczającym koniec bloku instrukcji warunkowej. Ostatecznie w zapisie relacji dodajemy dwa równania: jedno określające minimalną długość sprężyny jako iloczyn średnicy profilu i liczby zwojów, a drugie definiujące minimalny skok sprężyny jako równy średnicy profilu. Dzięki temu rozwiązaniu, gdy wprowadzona długość sprężyny doprowadziłaby do przenikania się zwojów sprężyny, zastosowane zostaną warunki minimalne definiujące geometrię sprężyny w stanie maksymalnie ściśniętym. (Wartość D5 w poniższych relacjach oznacza średnicę przekroju).
Podsumowanie
Równania matematyczne w postaci relacji Creo Parametric umożliwiają dokładniejszą kontrolę nad zachowaniem się geometrii oraz pełniejsze wykorzystanie parametryczności modelu. Zapisując odpowiednie równania oraz wykorzystując dodatkowe parametry możemy w znacznie większym stopniu wpłynąć na projekt oraz ułatwić wprowadzanie przyszłych zmian. Dzięki relacjom zyskujemy dodatkową pewność, że zaprojektowany model będzie się zachowywał w sposób przewidywalny i zgodny z założeniami projektowymi.